The kernel of the algorithm is the function that draws the visible part of a segment and updates the list of available spans. To see how it works let's say we have to draw a segment (xa,xb) and let's check how this segment may interact with a span (x0,x1):

Segment-span interaction types This picture shows all the possible interactions between a segment (xa,xb) and an available span (x0,x1).

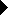	Case 1: x1 <= xa In this case we can simply ignore the available span and go to the next span on the scanline.
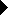	Case 2: x0<xa; xa<x1<=xb In this case the visible part is (xa,x1) and the span has to be updated setting the right limit at xa.
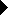	Case 3: x0<xa; x1>xb This is the worst case and requires the drawing of (xa,xb), the modification of the right end of the available span (setting it to xa) and the creation of a new available span (xb,x1). However after this operation there's no point in checking other spans on the scanline (spans on a scanline never overlap).
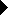	Case 4: x0>=xa; x1<=xb In this case the visible part is (x0,x1) and the span can be removed from the list of available spans. The algorithm must however continue the search for more eventual available spans on the same scanline.
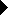	Case 5: xa<x0<xb; x1>xb In this case the visible part is (x0,xb) and the left end of the span has to be modified in xb. After that this scanline is completed.
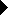	Case 6: x0>=xb This case doesn't require any drawing and informs that no more checks on this scanline are needed.

The following function draws the visible parts of a segment and updates the span list of the scanline. It's the C translation of the cases described above.

void DrawSegment(int y,int xa,int xb)
{
  Span *old,*current,*n;
  for (old=NULL,current=FirstSpan[y];
       current!=NULL;
       old=current,current=current->next)
  {
    if (current->x1<=xa) // Case 1
      continue;
    
    if (current->x0<xa)
    {
      if (current->x1<=xb) // Case 2
      {
        DrawPart(y,xa,current->x1);
        current->x1=xa;
      }
      else // Case 3
      {
        DrawPart(y,xa,xb);
        n=NewSpan();
        n->next=current->next;
        current->next=n;
        n->x1=current->x1;
        current->x1=xa; n->x0=xb;
        return;
      }
    }
    else
    {
      if (current->x0>=xb) // Case 6
        return;
      
      if (current->x1<=xb) // Case 4
      {
        DrawPart(y,current->x0,current->x1);
        n=current->next; FreeSpan(current);
        if (old) old->next=n;
            else FirstSpan[y]=n;
        current=n;
        if (current==NULL) return;
      }
      else // Case 5
      {
        DrawPart(y,current->x0,xb);
        current->x0=xb;
      }
    }
  }
}